Datenstrukturen und ein Algorithmus zur Triangulation zweidimensionaler Polygone

Triangulation für pointsandfaces.

Die Aufgabe

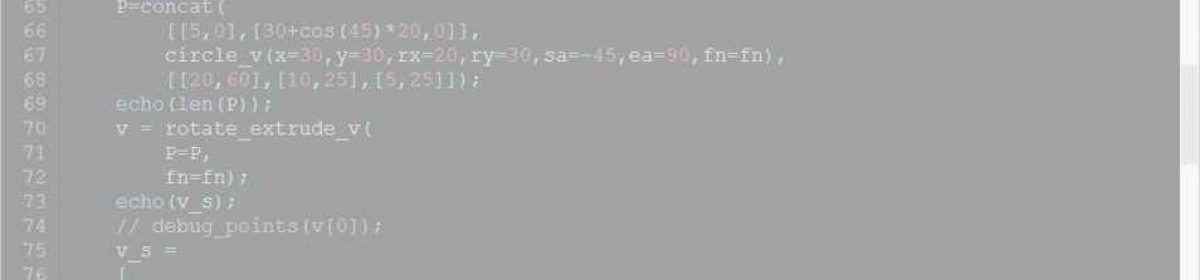
Gegeben ist ein Feld von Punkten (x,y), das die Punkte des Umrisses des Polygons im Uhrzeigersinn enhält.

Zu ermitteln ist ein Feld von Dreiecken, die zusammen genau die gesamte Fläche des Polygons ausfüllen, sich nicht überlappen und die mit jeder Kante an genau einer oder null Kanten anderer Dreiecke liegen. Letzteres betrifft z.B. die Punkte (30, 33, 34, 35), die auf einer Linie liegen, aber nicht ein Dreieck bilden dürfen, sondern in zwei Dreiecke aufgeteilt werden müssen, damit das Dreieck (30, 31, 33) eine ganze Kante mit seinem Nachbarn (30, 33, 35) teilt. Das wäre mit dem Dreieck (30, 34, 35) nicht möglich.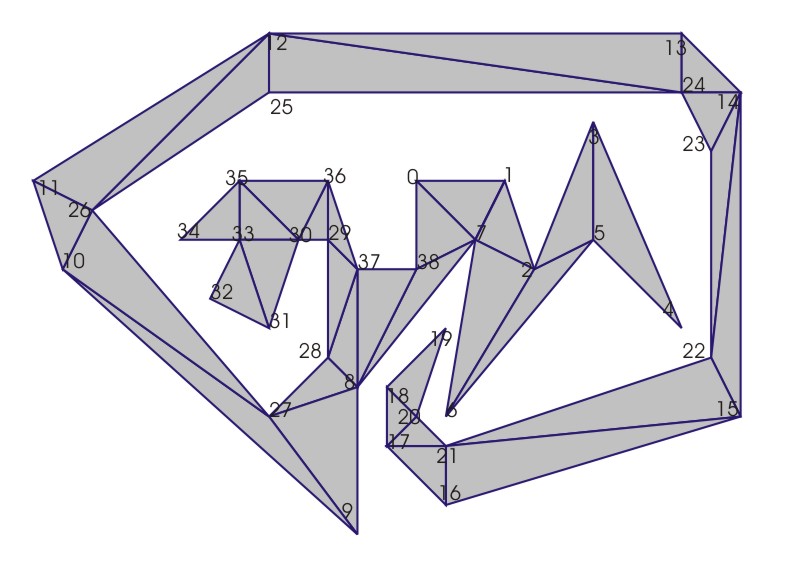

Lösungsansatz

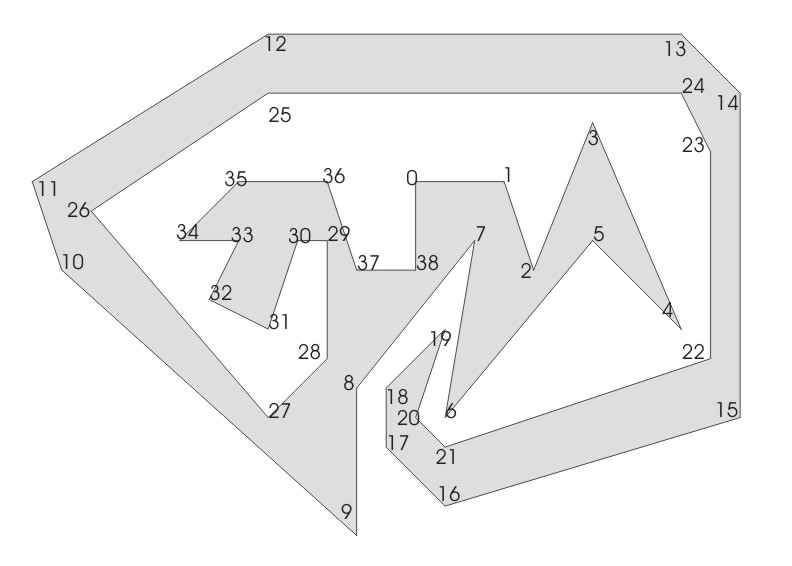
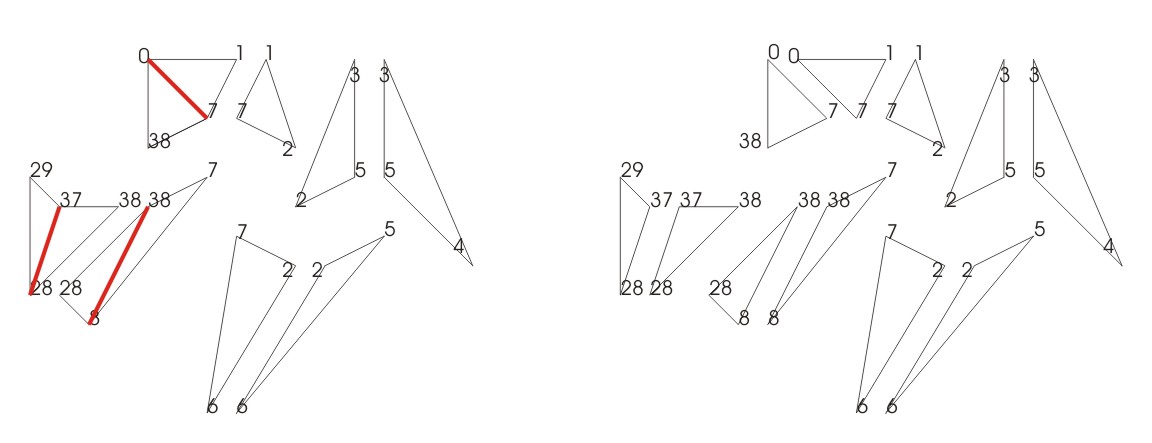
Der Lösungsansatz ist rekursiv. Das Polygon wird an zwei Punkten, deren Verbindungsgerade sich vollständig auf der Fläche des Polygons befindet, in 2 Hälften getrennt. Besteht eine Hälfte aus drei Punkten, wird sie in die Ergebnisliste übernommen, ansonsten wird mit beiden Hälften rekursiv weiter so verfahren.

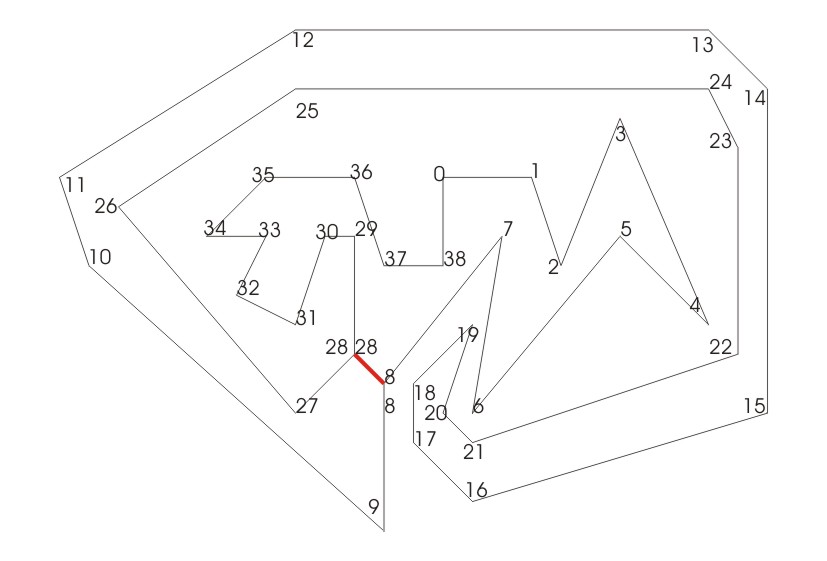
Zwischen den Punkten 8 und 28 wird getrennt

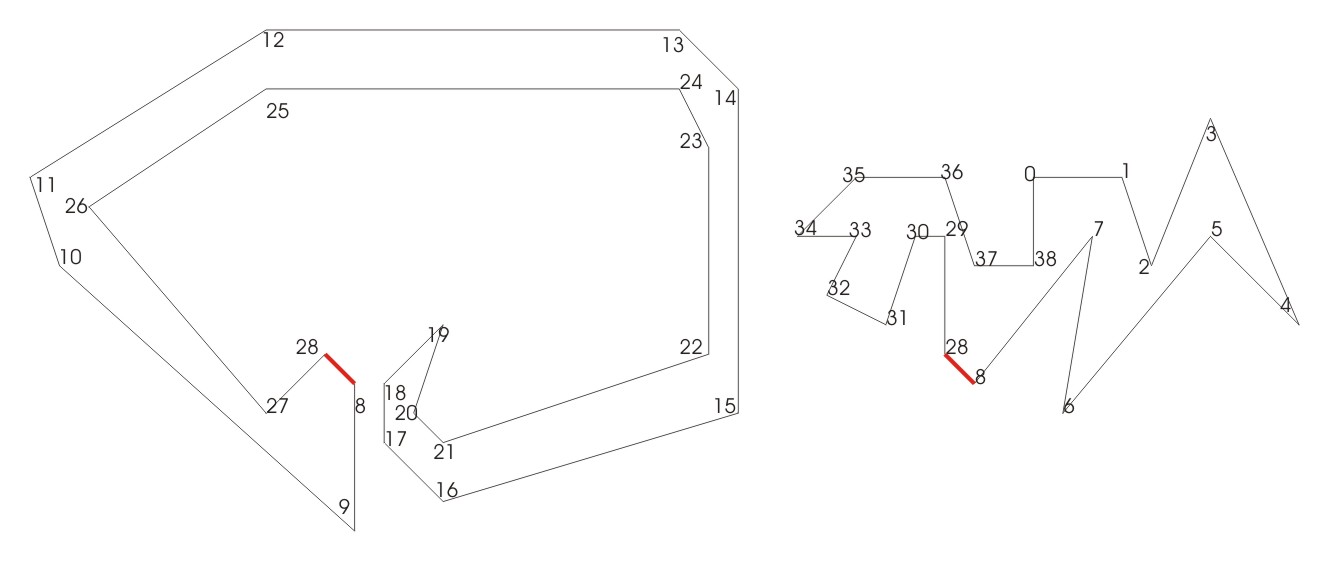
Zur besseren Darstellung sind die beiden entstehenden Polygone auseinander geschoben.

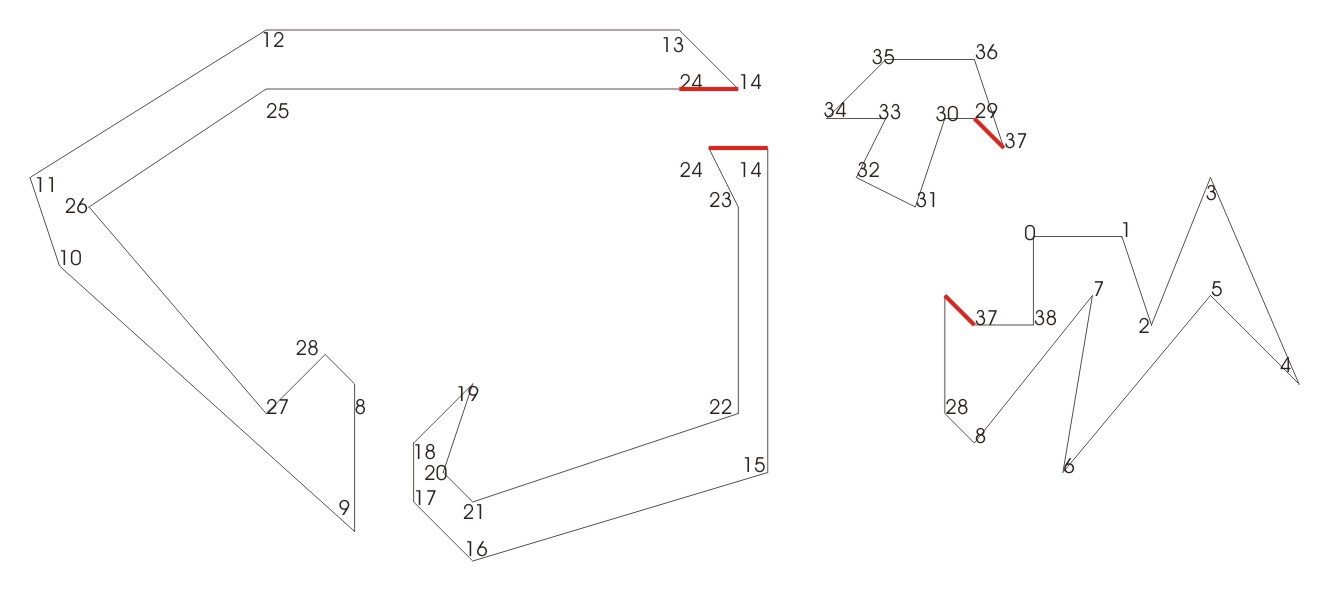
Die beiden Polygone werden jeweils wieder aufgetrennt, das eine zwischen den Punkten 14 und 24, das andere zwischen den Punkten 37 und 29.

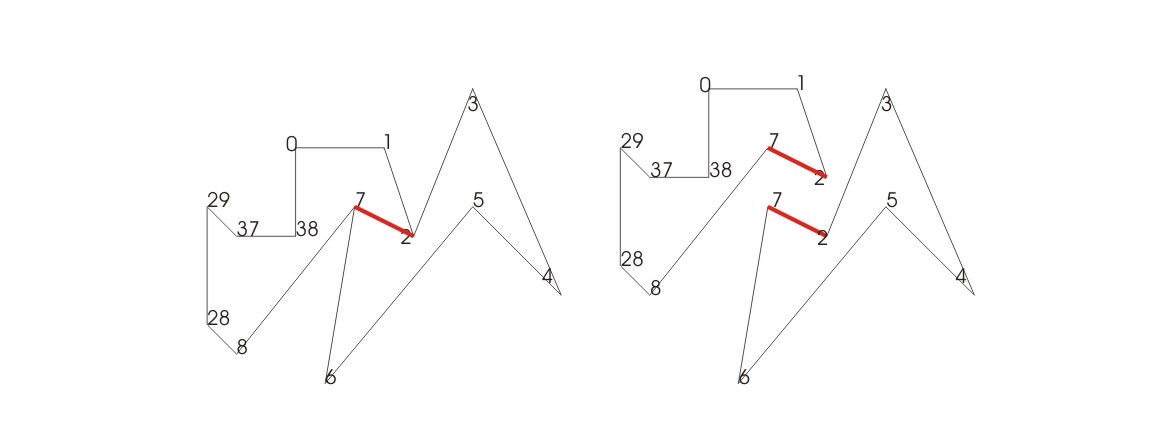
Zur besseren Übersicht wird hier nur ein Teil von den Vieren weiter trianguliert.

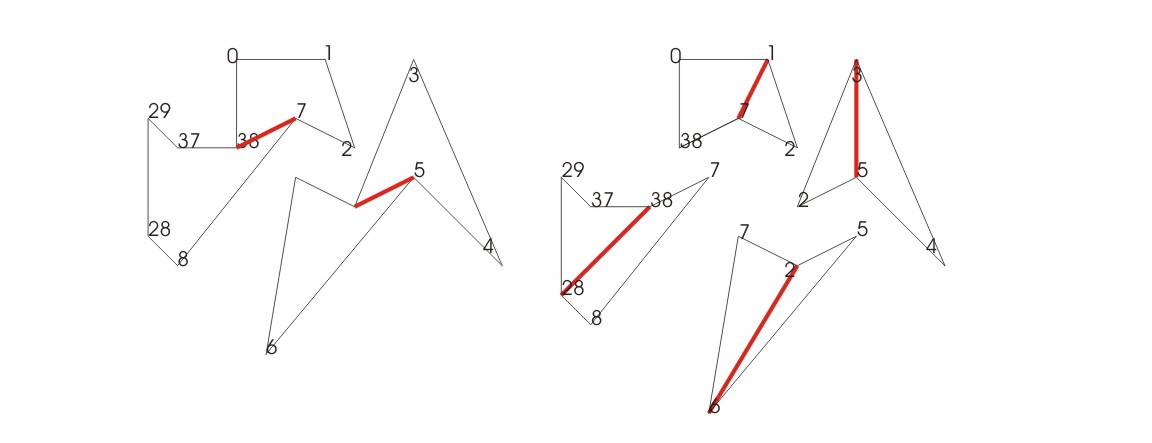
Bis nur noch Dreiecke vorhanden sind.

Datenstrukturen

Die Eckpunkte des Polygons sind im folgenden v_p:

v_p = [
 [ 25,  15], [ 40,  15], [ 45,   0], [ 55,  25], [ 70, -10], [ 55,   5], 
 [ 30, -25], [ 35,   5], [ 15, -20], [ 15, -45], [-35,   0], [-40,  15], 
 [  0,  40], [ 70,  40], [ 80,  30], [ 80, -25], [ 30, -40], [ 20, -30], 
 [ 20, -20], [ 30, -10], [ 25, -25], [ 30, -30], [ 75, -15], [ 75,  20], 
 [ 70,  30], [  0,  30], [-30,  10], [  0, -25], [ 10, -15], [ 10,   5], 
 [  5,   5], [  0, -10], [-10,  -5], [ -5,   5], [-15,   5], [ -5,  15], 
 [ 10,  15], [ 15,   0], [ 25,   0]
];

Ein (Teil-)Polygon wird durch ein Feld von Indizes auf P dargestellt und wird im allgemeinen v_ndx genannt:

v_ndx = [0, 1, 2, …, 36, 37, 38];

Um zu ermitteln, ob sich eine Gerade mit einer der Geraden, die das Polygon begrenzen schneidet, müssen alle einzeln untersucht werden, und zwar jedes mal, wenn das Polygon über die Gerade zwischen zwei Punkten in zwei Hälften geteilt werden soll. Es ist also sinnvoll, die Menge der möglichen Geraden, die in folgendem Bild gezeigt werden, in einer passenden Datenstruktur abzulegen und dann jeweils darin passende Geraden zu suchen.

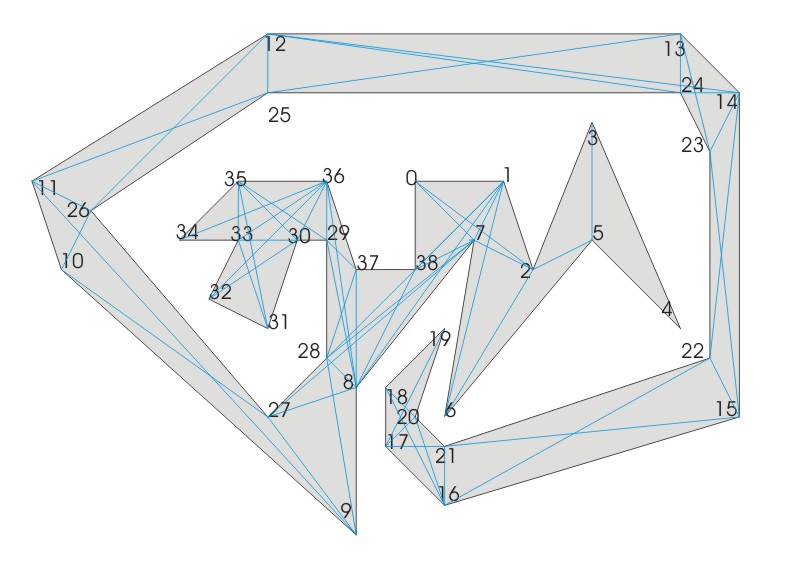
Wir brauchen eine mehrdimensionale Datenstruktur, v_lok (lines ok):

Die einzelnen Punkte sollten direkt indizierbar sein (1. Ebene), und zu jedem Punkt können mehrere Zielpunkte existieren (2. Ebene), und zu jedem Zielpunkt gibt es eine Entfernungsangabe, so dass eine 3. Ebene notwendig ist.

v_lok =
[ 
        // index 0, also Punkt 0
    [
        [
            2, // Ziel 
            25 // Entfernung
        ],
        [
            7, // Ziel
            14.1421 // Entfernung
        ],
    ],
        // Index 1, also Punkt 1
    [
        [
            6,  // Ziel
            41.2311// Entfernung
        ],
        [7, 11.1803],
        [8, 43.0116],
        [38, 21.2132],
    ],
…
]

Mathematische Grundlagen

Um v_lok zu ermitteln, müssen für jeden Punkt die anderen Punkte als mögliche Zielpunkte geprüft werden. Dabei können benachbarte Punkte auf den Umrissen des Polygons ausgeschlossen werden.

Am wichtigsten sind danach 2 Prüfungen:

Geht die Gerade vom Startpunkt aus in Richtung der Innenseite des Polygons?
Kreuzt die Gerade keine Umriss-Gerade?

Die erste Prüfung ist eine Frage des relativen Winkels der Geraden in Relation zu den beiden Umriss-Geraden, die an den betreffenden Punkt anschließen.

Um Winkel aus Positionen zu errechnen, benutzen wir die Funktion atan2(y,x), die den Parameter y durch den Parameter x dividiert, und vom Quotienten, der der Steigung relativ zur x-Achse entspricht, den Arcussinus aufruft. Diese Funktion handhabt den Sonderfall, der eintritt, wenn x gleich null ist, was eine Division durch null ergeben würde, aber abgefangen wird. Wenn für x null übergeben wird, wird für positive y 90, und für negative y -90° zurückgegeben.

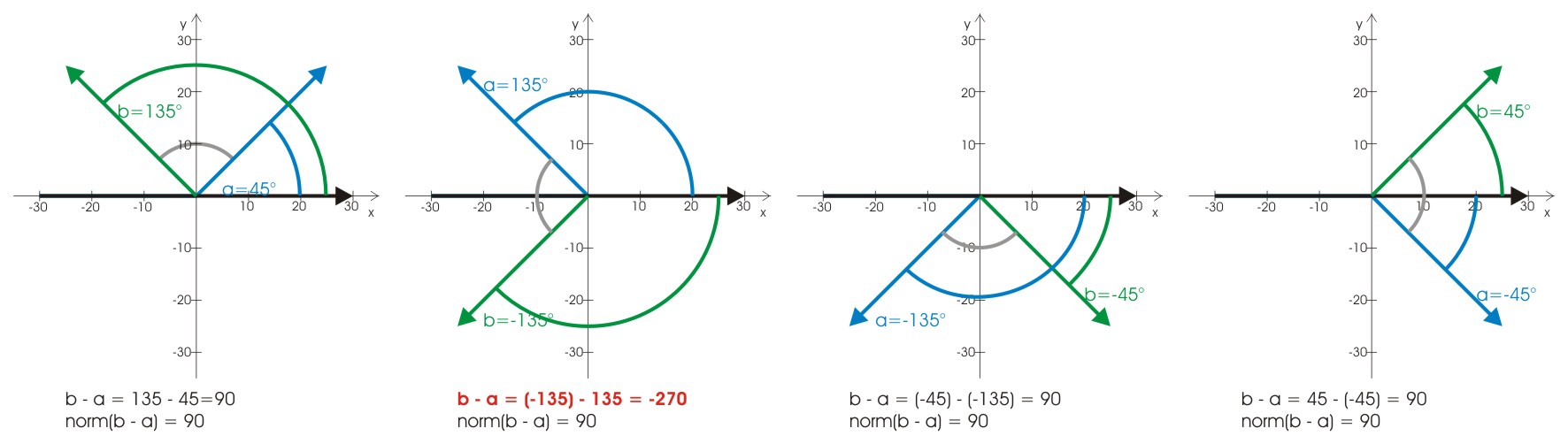
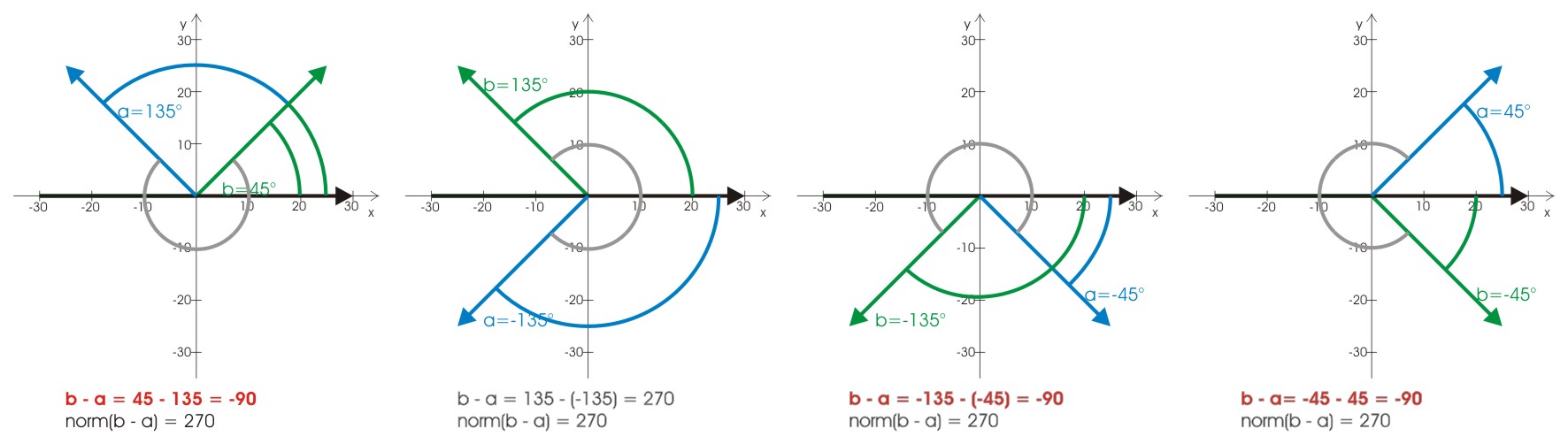
Wir interessieren uns aber gar nicht für Winkel in Relation zum Koordinatenkreuz, sondern die relativen Winkel der betroffenen Geraden zueinander, so dass wir von rechts und links sprechen können. Der Ergebnisbereich der Funktion atan2() geht von -180° bis 180°, wenn wir also zwei Winkel subtrahieren, um einen relativen Winkel zu erhalten, bekommen wir einen Ergebnisbereich von -360° bis 360°, den wir erstmal für uns normalisieren müssen, um Winkel in Relation zu setzen. Wenn wir folgende Bilder betrachten, sehen wir, dass es ausreicht, auf den Bereich von 0° bis 360° zu normalisieren, indem wir 360° addieren, durch 360 teilen und den Divisionsrest als Ergebnis nehmen

function pnf_corner_angle(P0,P1,P2) =
let
(
    dx1 = P1[0]-P0[0],
    dy1 = P1[1]-P0[1],
    dx2 = P2[0]-P1[0],
    dy2 = P2[1]-P1[1],
    angle1 = atan2(dy1,dx1),
    angle2 = atan2(dy2,dx2)
)
((angle2-angle1)+360)%360;

Relativer Winkel 90°:

Relativer Winkel 180°:

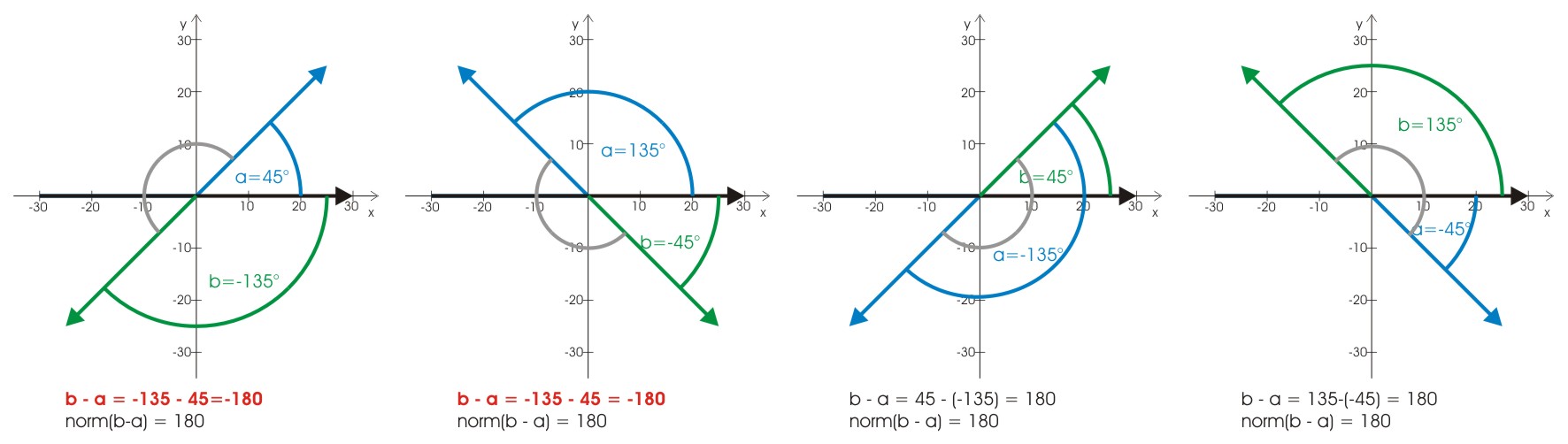
Und relativer Winkel 270°:

Schauen wir uns den einfachsten Fall, nämlich dass alle Winkel positiv sind, an:

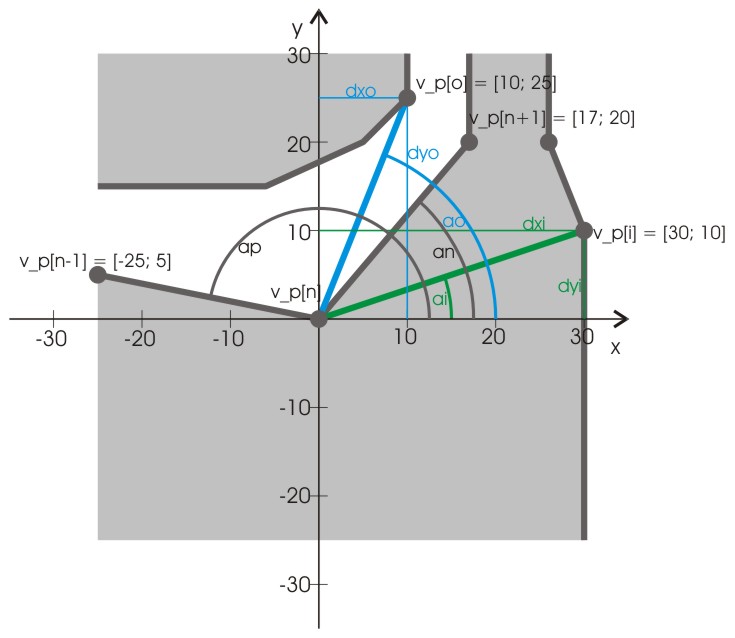
ai = atan(10,30) = 18.4349
an = atan(20,17) = 49.6355
ao = atan(25,10) = 68.1986
ap = atan(5,-25) = 168.69

Der Winkel ai, den die von Gerade v_p[n] nach v_p[i] geht, ist kleiner, als der Winkel, den die Gerade nach v_p[n+1] beschreibt. Solange wir nur die obere Hälfte des Koordinatenkreuzes betrachten und somit nur positive Winkel haben, reicht dies aus, um zu sagen, dass die Gerade nach v_p[i] rechts des weiteren Pfads liegt. Trotzdem bleibt weiterhin noch zu überprüfen, ob sie auch noch links hinter der Geraden liegt, die von v_p[n-1] nach v_p[n] geht, denn das muss auch wenn alle Winkel positiv sind nicht der Fall sein, wie folgendes Bild zeigt.

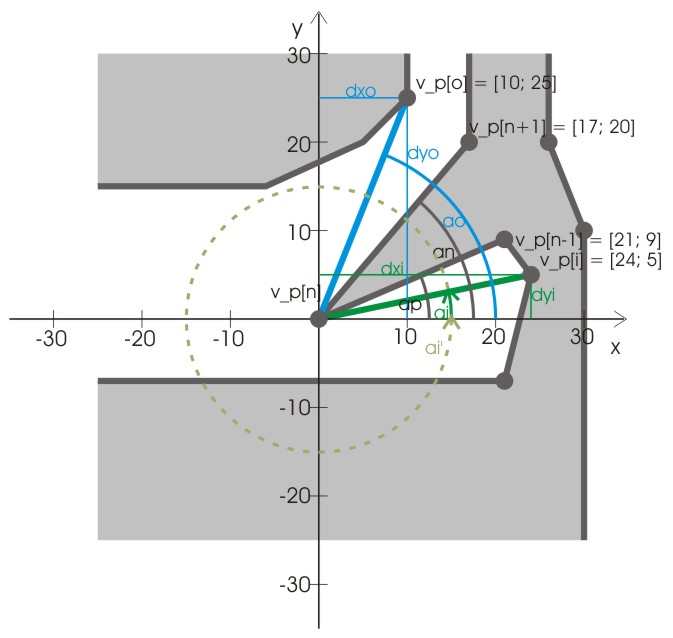
Hier ist der vorausgehende Punkt v_p[n-1] so positioniert, dass die Gerade nach v_p[i] das Polygon verlässt, obwohl ihr Winkel ai kleiner als ap ist.